矩形截面抗弯刚度,抗弯刚度

抗拉刚度EA是构件在拉力的作用下，抵抗拉伸压缩变形的能力抗拉刚度是构件在拉力的作用下，抵抗变形的能力，对长度相同，受力相同的杆件，EA越大则变形越小，亦称之为抗压刚度；题主是否想询问“框架结构梁柱的抗弯线刚度用什么符合表示”EIxEIy框架结构梁柱的抗弯线刚度用EIxEIy符合表示，E代表梁材料的弹性模量，Nmm^2，IxIy分别为梁截面对形心主轴x轴和y轴的截面抗弯惯性矩，mm^4抗弯刚度EIxEIy越大，荷载作用下梁的挠度就越小。

公式是 W=Mf 其中，M 是弯矩组合值，单位是N·mm通常需要组合风荷载产生的弯矩和地震作用产生的弯矩组合公式为M=Mw·05ME其中Mw为风荷载产生的弯矩值，ME为地震作用产生的弯矩值f为型材强度设计值 单位是Nmm#178，需要查表获得Mw的计算需要先求出风荷载的标准值，然后求出。

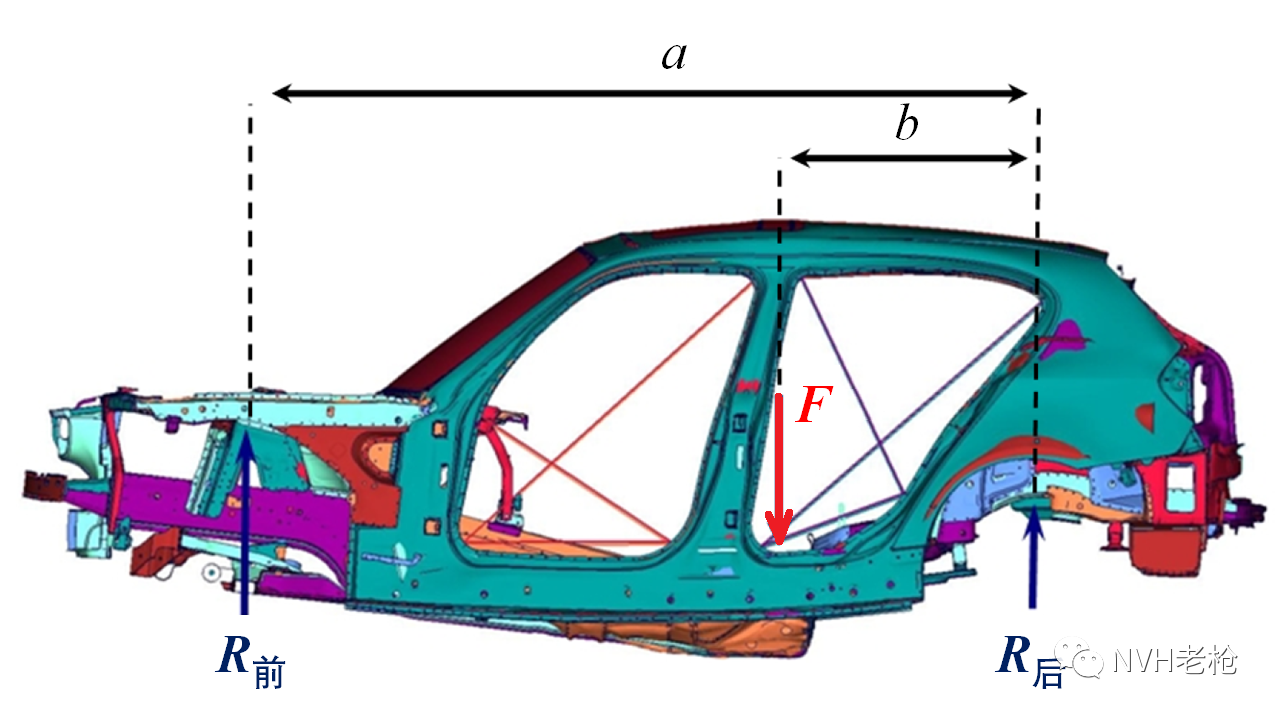
抗弯刚度单位

因此，可以说抗弯刚度是刚度的子集，专门用于描述物体在弯曲方向的抵抗性能具体到某些材料和结构，如金属梁建筑框架等，它们的抗弯刚度直接影响其整体的稳定性承重能力及使用寿命等性能而在更宏观的结构设计中，考虑整体的刚度对于保证结构的安全性和可靠性至关重要另外值得注意的是，不同的材料。

抗弯刚度计算公式是D=ET*3，抗弯刚度是指物体抵抗其弯曲变形的能力早期用于纺织抗弯刚度大的织物，悬垂性较差纱支粗，重量大的织物，悬垂性亦较差，影响因素很多，有纤维的弯曲性能纱线的结构还有织物的组织特性及后整理等抗弯刚度现多用于材料力学和混凝土理论中，其英文名称为bending。

织物刚柔性是指织物的抗弯刚度和柔软度是用于反映织品风格的重要指标，例如西装用织物要求挺括，保型性好内衣用织物要求手感柔软，穿着舒适夏季女装用织物要求飘逸柔美织物的刚柔性通常用抗弯刚度描述，抗弯刚度是指织物抵抗其弯曲方向形状变化的能力刚柔性的测定方法很多，其中最基础的方法是。

拉压刚度的计算公式是K=EI，而抗弯刚度的计算公式是D=3ET，抗弯强度=弹性模量×截面惯性矩，抗弯强度是指物体抵抗其弯曲变形的能力，弹性模量即产生单位应变时所需的应力抗弯刚度大的织物，悬垂性较差纱支粗，重量大的织物，悬垂性亦较差，影响因素很多，有纤维的弯曲性能纱线的结构还有织物的。

比如有一个和剪力墙高度相同的杆单元，下端固结，使剪力墙与杆单元顶端在相同的力作用下产生相同的位移，此时杆单元的刚度就是剪力墙的等效刚度刚度使结构顶端产生单位位移的力即K=FΔ 高层建筑在水平荷载作用下，剪力墙抗侧力有抗弯刚度抗剪刚度，都是由其截面的力学参数和材料的力学参数组成的。

抗弯刚度 R 是描述梁在弯曲时抵抗变形的能力的一个参数，通常用来衡量梁的刚度在弹性阶段，R 与弹性模量 E梁截面的惯性矩 I 以及梁的长度 L 有关一般来说，R 的计算公式可以表示为这个公式基于弹性理论，适用于梁在弯曲加载时处于弹性阶段的情况需要注意的是，如果梁经历了非弹性阶段即。

抗弯刚度抗剪刚度和抗扭刚度的计算公式如下1 抗弯刚度计算公式EI = E×截面惯性矩I其中，E代表材料的弹性模量，反映材料的弹性性能I是截面惯性矩，与截面形状和尺寸有关2 抗剪刚度计算公式KV = K×截面剪切刚度V其中，K是与截面形状有关的剪切系数V为剪切刚度，与材料的剪切。

抗弯刚度计算公式EI

首先，抗拉刚度EA，它是材料抵抗拉伸变形的能力的体现弹性模量E，通常称为杨氏模量，是衡量材料弹性强度的基础参数，根据材料的类型和特性，如钢材混凝土等，E会有不同的数值截面面积A则影响整体的抗拉性能，对于常见的矩形截面，A的计算公式是b乘以h，即A = b * h而抗弯刚度EI，则衡量材料。

在工程中抗弯刚度条件一般指核梁的挠度抗弯刚度是指物体抵抗其弯曲变形的能力早期用于纺织抗弯刚度大的织物，悬垂性较差纱支粗，重量大的织物，悬垂性亦较差，影响因素很多，有纤维的弯曲性能纱线的结构还有织物的组织特性及后整理等抗弯刚度现多用于材料力学和混凝土理论中，其英文名称为。

EA为拉压刚度，其中E为弹性模量，A为截面面积EI为抗弯刚度， 其中E为弹性模量，I为截面惯性矩以矩形截面为例EA=E*b*hEI=E*b*h^312。

抗弯刚度Bending Stiffness是衡量材料或结构抵抗弯曲变形的能力的一个物理量它通常与材料的弹性模量杨氏模量和结构的几何特性如截面惯性矩相关在工程和材料科学中，通常使用“刚度”来描述一个系统在施加一定外力或力矩时所表现出的变形抵抗能力抗弯刚度越高，表示材料或构件在受到弯曲载荷。

是的弯曲长度在数值上等于织物单位密度单位面积重量所具有的抗弯刚度的立方根，弯曲长度数值越大，表示织物越硬挺而不易弯曲抗弯刚度，物体抵抗其弯曲变形的能力是指物体抵抗其弯曲变形的能力早期用于纺织抗弯刚度大的织物，悬垂性较差纱支粗，重量大的织物，悬垂性亦较差，影响因素很多，有。